Numeracy
- mrsstrickey
- Nov 10, 2020
- 5 min read
What is numeracy?
The ability to use maths in real life context.
Comparing prices
Calculating a percentage discount
Reading Train Timetables
Estimating and assessing the validity of an answer
The ability to apply maths skills and use them in context is of increasing importance in the new maths curriculum.
The biggest myth about maths is that it is something that you either can or cannot do.
Maths is about pattern and an important part of feeling comfortable about maths is recognising the in-built patterns in number and number relationships.
Unfortunately these patterns often remain hidden – partly due to our strange (in English) numbering system.
For example, eleven, twelve, thirteen is ‘one ten and one’, ‘one ten and two’, ‘one ten and three’ in most Asian languages.
There are three main reasons why ‘I can’t do maths’ is so common:
It is culturally acceptable in the UK to say that you are ‘bad at maths’ - we hear it so often it doesn’t seem a strange thing to say. In some other countries (often ones that perform highly in maths) this is not the case.
When we come across maths problems that we can’t work out in our heads quickly, we often panic and say ‘I can’t do maths!’
When literacy levels are low, it makes it harder for the individual to understand what maths is required.
When we think of maths we may think of things like algebra or trigonometry, rather than everyday maths.
Numeracy is a proficiency which is developed not just in mathematics but also in other subjects. It is more than an ability to do basic arithmetic. It involves developing confidence and competence with numbers and measures. It requires understanding of the number system, a repertoire of mathematical techniques and an inclination and ability to solve quantitative or spatial problems in a range of contexts.
Numeracy also demands understanding of the ways in which data are gathered by counting and measuring, and is presented in graphs and diagrams, charts and tables
Being numerate helps us to function responsibly in everyday life and contribute effectively to society. It increases our opportunities within the world of work and establishes foundations which can be built upon through lifelong learning. Numeracy is not only a subset of mathematics; it is also a life skill which permeates and supports all areas of learning, allowing young people access to the wider curriculum.
We are numerate if we have developed:
the confidence and competence in using number which will allow individuals to solve problems, analyse information and make informed decisions based on calculations.
A numerate person will have acquired and developed fundamental skills and be able to carry out number processes but, beyond this, being numerate also allows us to access and interpret information, identify possibilities, weigh up different options and decide on which option is most appropriate.
Numeracy is a skill for life, learning and work. Having well-developed numeracy skills allows young people to be more confident in social settings and enhances enjoyment in a large number of leisure activities. For these and many other reasons, all teachers have important parts to play in enhancing the numeracy skills of all children and young people.
Numerate people rely on the accumulation of knowledge, concepts and skills they have developed, and continually revisit and add to these. All practitioners, as they make use of the statements of experiences and outcomes to plan learning, will ensure that the numeracy skills developed from early levels and beyond are revisited and refreshed throughout schooling and into lifelong learning.
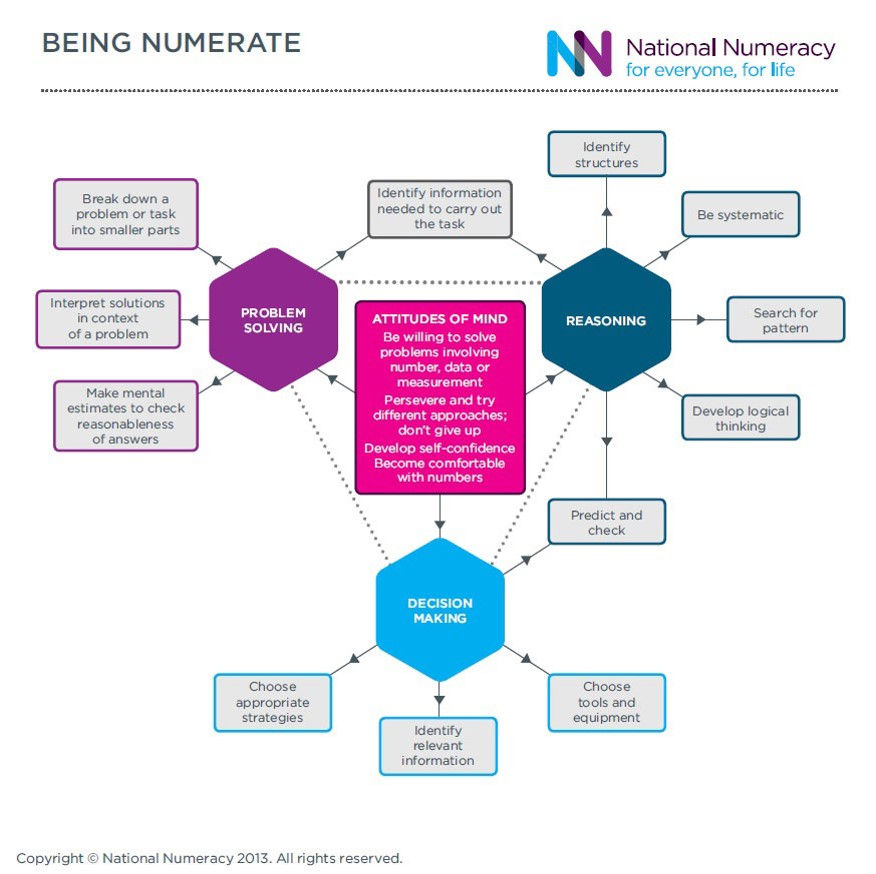
These are some of the ways mathematical thinking might naturally occur across the curriculum:
Identifying structures & relevant data
Being systematic
Searching for patterns
Thinking logically
Predicting & checking
Breaking down problems into smaller parts
Interpreting solutions in context of problem
Estimating to check likelihood of answers
These ways of holding the world are not only essential for an understanding of mathematics but also enrich every area of life. Here are some possibilities:
1. Sequencing
In order to help students think systematically, logically and to break down problems into smaller parts it helps to see things sequentially. Six Degrees of Separation (or The Kevin Bacon Game as it’s sometimes known), is useful way to get pupils to reflect on the explanations we’ve offered. If you’ve never encountered this before, it’s based on the theory that every human being in the world is connected to every other human being through a chain of no more than six people. The idea is that they need to logically sequence their understanding from one concept to another. We could provide pupils with a prompt connected to the topic we’re studying, give them an end point they have to connect to and get them to sequence what they know:
Select a topic or theme.
Write 1–6 along a timeline.
Put your topic at number 6.
Get from the stimulus to your topic in no more or less than six steps.
So we might ask them to suggest the six degrees of separation between the assassination of Archduke Ferdinand and the outbreak of the Great War, or between Pip’s first meeting with Magwitch and his discovery that he has ‘great expectations’. To keep them on track, we might specify that step 4 must be the introduction of Mr Jaggers, or the Ottoman-German Alliance or whatever. And if six degrees is too few or too many then feel free to extend the chain as far as you think it should stretch.
2. Asking mathematical questions
In most subjects there are times when we want students to consider what they’re learning about in a mathematical way. It might therefore be useful to ask them to frame question about curriculum content in mathematical terms:
How could you sort these…….?
How many ways can you find to ……. ?
What happens when we ……… ?
How many different ……. can be found?
What is the same/different?
Can you group these ……. in some way?
Is there a pattern?
How can this pattern help you find an answer?
What do think comes next? Why?
Is there a way to record what you’ve found that might help us see more patterns?
What would happen if….?
3. Domain specific thinking (with maths)
And asking these kinds of questions could help prompt student to think about subject content using the tools of mathematics:
specialising – trying special cases, looking at examples
generalising – looking for patterns and relationships
conjecturing – predicting relationships and results
convincing – finding and communicating reasons why something is true.
4. Organising information
The Venn Diagram useful way to organise and present information across a range of subjects.
One drawback though is that the overlapping space can be too cramped to contain much writing. An alternative is to use Comparison Alley where information is organised in such a way that there’s plenty of space to make the comparison:
5. Presenting information
Maths provides new and useful ways of seeing the world. Many if not most subject areas can find space to expand students’ thinking by asking them to express their understanding using the tools of mathematics. For instance I have on various occasions used each of the following in English lessons:
Graphs
Timelines
Flow charts
Graphic organisers
Pie charts
6. Seeing relationships
Size matters. Understanding how big something is in relation to something else can be important in all sorts of lessons. Another area where we might benefit from mathematical thinking is scale. A favourite example is how we can get students to wrap the head around how big a billion is:
A million seconds = 11 ½ days
A billion seconds = 32 years
7. Accuracy matters
Maths also has something to teach us about attention to detail, particularly the difference between ‘getting it right’ and ‘getting it done’. Where can we apply the concept of ERROR CHECKING across the curriculum?
Dates in history?
Notation in music?
Learning lines in drama?
Punctuation in English?
Further Reading




toto slot, toto slot, toto slot, toto slot, toto slot, raja168, raja168, raja168, raja168, raja168, toto slot, toto slot, toto slot, toto slot, toto slot, toto slot, toto slot, toto slot, toto slot, raja168, raja168, toto slot, toto slot, toto slot, toto slot, raja168, toto slot,
slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, raja168, raja168, raja168, raja168, raja168, raja168, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, raja168, raja168, raja168, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, raja168, slot gacor, raja168, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, raja168, raja168, slot gacor, raja168, slot gacor, slot gacor, slot gacor, slot gacor, slot gacor, raja168,
slot qris, slot deposit dana, link slot